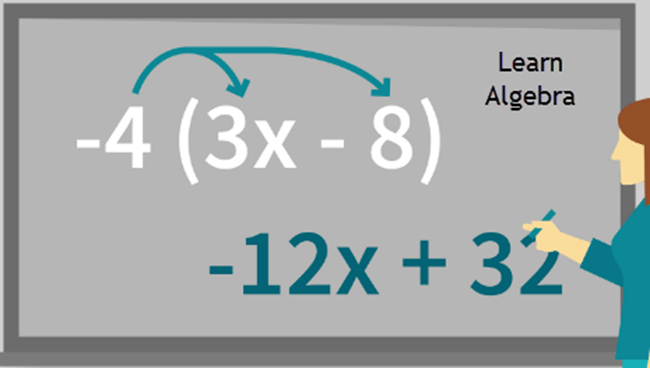Pre-Algebra Made Easy: The Complete Beginner’s Guide
Introduction: Why Pre-Algebra Feels Hard (and How to Make It Easy)
If the phrase pre-algebra makes your palms sweat, you’re not alone. Many beginners see it as a confusing maze of numbers, symbols, and rules. But here’s the truth: pre-algebra is not about memorizing formulas—it’s about learning a new language that helps you think logically and solve real-world problems.
This article, “Pre-Algebra Made Easy: The Complete Beginner’s Guide,” is your roadmap. Whether you’re a student brushing up before algebra, a parent helping your child, or even an adult learner returning to math after years away, this guide will break everything down step by step. By the end, you’ll see pre-algebra not as a barrier, but as a bridge to confidence in mathematics.
What Is Pre-Algebra, Really?
Pre-algebra is the transition stage between basic arithmetic (addition, subtraction, multiplication, division) and formal algebra. It introduces the concepts that prepare you for equations, variables, and advanced problem-solving. Think of it as the “training wheels” of algebra.
Here are the key skills you’ll find in pre-algebra:
- Working with whole numbers, fractions, and decimals
- Understanding negative numbers
- Learning factors, multiples, and prime numbers
- Introduction to variables (like x and y)
- Order of operations (PEMDAS)
- Ratios, proportions, and percentages
- Basic geometry concepts
- Simple equations and inequalities
These skills may look intimidating on paper, but with practice, they start to feel natural.
Why Learning Pre-Algebra Matters
1. Foundation for Higher Math
You can’t run before you walk, and you can’t tackle algebra, geometry, or calculus without mastering pre-algebra. It’s the backbone of all advanced math.
2. Real-Life Applications
Far from being abstract, pre-algebra shows up in everyday life:
- Splitting a restaurant bill fairly
- Calculating discounts during shopping
- Comparing mobile data plans
- Converting recipes in cooking
3. Boosts Problem-Solving Skills
Pre-algebra trains your brain to think in steps, recognize patterns, and make logical decisions—skills that are useful beyond math, even in business or tech.
Pre-Algebra vs. Arithmetic: What’s the Difference?
| Aspect | Arithmetic | Pre-Algebra |
|---|---|---|
| Focus | Basic operations: +, –, ×, ÷ | Extending concepts with variables, negatives |
| Numbers Used | Whole numbers, fractions, decimals | Whole numbers + negatives, unknowns (x, y) |
| Thinking Style | Direct calculation | Abstract reasoning & logical steps |
| Example | 5 × 6 = 30 | Solve for x: 5x = 30 → x = 6 |
Pre-algebra shifts you from simply crunching numbers to understanding why numbers work the way they do.
Breaking Down Core Pre-Algebra Topics
1. Numbers and Operations
Before moving into equations, pre-algebra makes sure you’re comfortable with:
- Integers: Positive and negative whole numbers
- Absolute Value: Distance of a number from zero (|–5| = 5)
- Factors and Multiples: Essential for simplifying fractions
👉 Tip: Use number lines to visualize negatives—it helps beginners grasp the concept faster.
2. Order of Operations (PEMDAS)
You may remember this acronym:
Parentheses → Exponents → Multiplication → Division → Addition → Subtraction
Example:
Solve: 3 + 2 × (4 – 1)
= 3 + 2 × 3
= 3 + 6
= 9
This rule prevents confusion and ensures everyone gets the same result.
3. Fractions, Decimals, and Percents
Pre-algebra connects these three forms of numbers:
- ½ = 0.5 = 50%
Understanding conversions is critical for real-world problem-solving, like calculating discounts or analyzing data.
4. Variables and Simple Equations
The first time you see “x” in math, it feels mysterious. But variables are simply placeholders for numbers.
Example:
Solve 2x + 4 = 10
→ Subtract 4 from both sides: 2x = 6
→ Divide by 2: x = 3
Once you grasp this, algebra starts feeling like solving puzzles.
5. Ratios and Proportions
Ratios compare two values. Proportions show equality between ratios.
Example:
If 2 pencils cost $1, how much do 10 pencils cost?
2:1 = 10:x
Cross multiply → 2x = 10 → x = 5
6. Geometry Basics
Pre-algebra introduces shapes, perimeter, area, and volume. These aren’t just for exams—they show up in real-life design, construction, and even art.
Common Struggles (and How to Overcome Them)
- Fear of Word Problems
👉 Fix: Translate words into math step by step. For example, “three more than twice a number” becomes 2x + 3. - Mixing Up Negatives
👉 Fix: Use real-life analogies like money or temperature. If it’s –5°C and the temperature drops 3 degrees, you’re at –8°C. - Skipping Steps
👉 Fix: Write down every step of your solution. Math rewards clarity and patience. - Lack of Practice
👉 Fix: Practice a little daily. Even 15 minutes keeps concepts fresh.
How to Learn Pre-Algebra Effectively
1. Start With Real-Life Examples
Before teaching fractions, show how a pizza is cut. For percentages, use shopping discounts. Connecting math to daily life makes it less abstract.
2. Use Visual Tools
- Number lines
- Pie charts for fractions
- Bar models for proportions
3. Leverage Online Resources
Websites like Khan Academy or Math is Fun provide interactive lessons and practice problems.
4. Practice With Games
Apps like Prodigy or DragonBox turn math practice into fun challenges, especially for kids.
5. Ask “Why” Instead of Memorizing
Instead of just memorizing formulas, dig into why they work. For example, why does dividing by a fraction mean multiplying by its reciprocal? Understanding prevents confusion later.
Personal Experience: Learning Pre-Algebra as an Adult
When I returned to math after years away, I felt intimidated by symbols and rules I had forgotten. But I discovered something powerful: breaking problems into small, logical steps made them less scary.
For example, solving an equation like 3x + 7 = 16 seemed impossible at first. But when I learned to treat it like balancing a scale—whatever I subtract on one side, I subtract on the other—it suddenly made sense. That “aha!” moment showed me pre-algebra isn’t about speed or memorization—it’s about building a mindset of patience and logical problem-solving.
Pre-Algebra Study Plan for Beginners
| Day | Topic | Activity |
|---|---|---|
| Day 1 | Integers & Number Line | Practice with temperature changes |
| Day 2 | Fractions & Decimals | Convert recipes (½ cup → decimals) |
| Day 3 | Order of Operations | Solve 10 practice problems |
| Day 4 | Ratios & Proportions | Compare prices at grocery store |
| Day 5 | Basic Equations | Solve 5 one-step problems |
| Day 6 | Geometry Basics | Measure items at home |
| Day 7 | Review & Real-Life Application | Apply concepts in budgeting or shopping |
This structure builds confidence step by step without overwhelming you.
Conclusion: Turning Fear into Confidence
Pre-algebra doesn’t have to feel like a monster under the bed. With the right mindset, resources, and consistent practice, anyone can master it. This guide, “Pre-Algebra Made Easy: The Complete Beginner’s Guide,” gives you the tools to see math as a skill you can build, not a talent you’re born with.
The next time you see an equation, remember—it’s not a wall. It’s a doorway to new ways of thinking.
What you will learn?
Understand and apply the core concepts of arithmetic & its uses.
Online learning platform
Fractions with Proper, Improper and Mixed
Decimals and Percentages with value to percent and vice versa.
Grasp the fundamentals of integers, exponents & Powers, and square roots.
Long Division Method to solve Square roots
Basic understanding of Geometry with shapes, area, perimeter, Volume and Angles
Basics of Logarithms
Solve real-world problems using basic pre algebraic principles.
Master the building blocks for success in algebra and higher-level math courses.